When a Systems Theorists such as Kenneth Boulding (here) looks at the Malthusian Model he sees a General System, an interaction between population growth and economic development. When an Economist such as Harvey Leibenstein (here) looks at the model, he sees an Error Correcting Controller (ECC) for population and economic growth--sometimes Economists call the ECC a Stock Adjustment Model and use it for inventory modeling. When John Maynard Keynes looked at the Malthusian model, he saw a way to rebuild Economics on a more empirical basis rather than on Ricardian Theoretical Ideas (see Stefan Eich's analysis here and also note that Karl Marx's economic model and Neoclassical Economic Theory were both based on Ricardo).
Why then is the Malthusian model so widely reviled even hated (Marx was harshly and implacably critical of Malthus and his ideas)? There are many reasons but basically Malthus was ahead of his time in the Social Sciences, articulating a model that was simple, easily testable and easily falsifiable. The assertion that population grows exponentially and agricultural production (subsistence) grows linearly (creating an eventual crisis), can be easily tested and rejected. In general, it didn't happened because of technological change in Agriculture.
Thomas Robert Malthus (1766-1834) had the misfortune of living during a period when the tools of the Classical Economists involved lengthy, obscure writings and poorly articulated mental models of the Economy. Abstract ideas were never given operational definition and as a result were untestable. Today, we have better tools to develop and test statistical models on historical data. When we read the Classics we need to salvage what is useful for model building and statistical testing.
Harvey Leibenstein (1922-1994) did just that and developed the following equation which summarized Malthusian ideas:
where S is the system state at time t, Q is production, N is population and the c are constants.
As a causal directed graph (above), Technology (TECH) and dynamics (self-loops) for both Q and N can be added.
In a future post I'll define TECH better and test the entire Malthusian model during a specific period in a specific country, but first let me just concentrate on the Malthusian ECC on the right of the graph, S. Your first question should be "does the Malthusian ECC describe any historical period in a given country?". It actually describes many periods in many countries, but let me start with one I know well, Germany in the Late 19th Century.
The first line in the Measurement Matrix, above, describes overall growth in the system, Malthus1 = (0.707 QA + 0.707 N), and explains 87% of the variation in the two indicators. The second line of the Measurement matrix captures the Malthusian controller, Malthus2 = (0.707 QA - 0.707 N), and captures another 13% of the variation in Q and N, explaining all the variation.
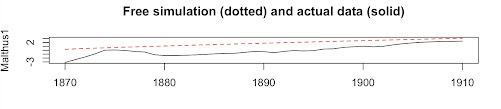
A time plot of Malthus2 (above) shows that right after German Unification in 1872, there was a Malthusian Crisis (QA-N < 0) that ran from Unification until almost 1880. The dashed red line in the graphic above is the attractor path for the Malthusian model, an approximate straight line around (QA-N = 0).
The result of this bounded Malthusian Crisis in Germany was that more than 5 million Germans emigrated to the US during the Late 19th Century, migration being one of the ways to alleviate Malthusian Pressure. European Emigration can be explained with other "pull factors" from the New World, but there also have to be "push factors," and Malthusian Pressure can be one. It is hard not to interpret the current Emigration from Africa to Europe as predominantly Malthusian Pressure, but it can be tested using the model above.
But what about Malthus1 that explains 87% of the variation in Q and N? The graphic above indicates that the Malthusian growth component was underperforming below the attractor path for most of the late 19th Century in Germany. Germany's late and rapid growth and Modernization, thought to be a factor in World War I, was basically a return to the attractor path interrupted by German Unification.
A question I'll answer in a later post is whether German development in the Late 19th Century had anything to do with feedback from the post-Unification Malthusian crisis? In other words, was there any feedback between Malthus2 and Malthus1? Answering the state-feedback question involves a more complicated causal direct graph (above) but can be handled easily by a state space model.
The mistake made by critics is to view the Malthusian ECC (Malthus2) as an all-or-nothing explanation. Clearly, it isn't. The ECC model above only explains 13% of the variation and we have only included two indicators, QA and N. In future posts, I will explain how the Malthusian Controller can be generalized to other controllers (for example, the Marxian controller (Q-W) and embedded within larger models. For the time being, my point is that we should salvage the Malthusian ECC from Classical arguments and realize that (1) it is one of many ECCs that exist within Modern Societies, (2) it still remains important for most pre-Industrial, pre-market societies that don't fit the Neoclassical Growth Model (as pointed out by Unified Growth Theory) and (3) it does provide, as Keynes thought, a way to rebuild economic models on more empirical footing.
In the mean time, if you want to run the DEL19 Malthusian model yourself, it is available here.
Methodology
The coefficients in the Malthusian Measurement matrix (above) were not plucked out of thin air or guesstimated but rather statistically estimated using Principle Components Analysis. The attractor path (dashed red line) was simulated using the DEL19 Malthusian model estimated with the dse package in the R programming language. You can run the DEL19 Malthusian model on line here using the Snippets web service.







No comments:
Post a Comment