What is Neoliberalism?

 

Quinn Slobodian (2020) has written a recent book Globalists: The End of Empire and the birth of Neoliberalism. I'm in the process of reading it and the book has changed my perspective on Neoliberalism. In 2018, I had been working on developing a "Neoliberalism Index" but I just couldn't capture the concept with a reasonable number of indicators. So, I decided it was really a hierarchical-concept that was best expressed by a number of indexes (see the hierarchy diagram above). But my concept of Neoliberalism was based purely in the American (Reagan) and British (Thatcher) popular political version. Slobodian opened my eyes to the wider intellectual history that dates back to WWI, the Great Depression and WWII. Let me report how I see Neoliberalsim now and how I think it might be destroyed by the two Trump Administrations which have just come to power again in the US.

First, let's recall how Germany destroyed the Liberal International Order by it's pursuit of World Domination during WWI. The World System and how it was to be reconstructed after WWI was a primary concern of the European Neoliberals. Tracing these concerns helps us understand what WWI was actually about and the role that the World System played in it and continues to play in Geopolitical Alignment.

I have constructed indexes for each of the Neoliberal components: Austerity, Globalization, Financialization, Debt, Hardship, IMF_Pressure and the Ecological Footprint. You can see some of these indexes at work in Shefner et. al. (2015). In future posts I will bring these indexes up to date for other countries in the World-System. My main questions are whether the Neoliberal World Order will be over after the Trump Administrations and what that might mean for the future.

In the meantime, I would recommend reading Globalists: The End of Empire and the birth of Neoliberalism.

World-System (1872-1908) Germany in the World System

 

World-System (1872-1908) Expanded Outputs of the Classical Model for Germany

 

In a prior post (here) I tested Higgins (1968) Classical Model on Germany in the late Nineteenth Century. The Higgins model had a number of shortcomings, particularly in the output variables. A market wasn't included and designating Capital as the only Capitalist output could equally be applied to a State Capitalist model and a market based Capitalist system. In this post, I will expand Higgins for Germany and see where it takes us.

Higgins model did allow us to define the essential variables and construct a system state for the Classical model. We can now break out any variables we want and consider them as outputs. The two I will deal with in this post are the Marxist model and the Market model (see the graphic above).

Even though Capital was the primary output for Marx, it is also clear that Ownership was also very important and had to be removed from private hands for the Communists State to emerge. So, let's add a measure of ownership, the GINI Coefficient, to the model. The coefficient is a percentage in the range [0,1] where zero indicates perfect equality (everyone owns an equal share of output) to one (100%) which indicates perfect inequality (Capitalists own al the Capital stock). A similar measure would be the Share of Wealth, another percentage with similar meaning. For Marx, a Capitalist system required not only investment in Capital stock but also a high degree of wealth concentration.

To capture Adam Smith's insights, we would need to add a free market as another output of the system.

World-System (1872-1908) A Classical Model of German Development

 

In a prior post (here), I discussed whether we should pay attention to the Classical Economists who wrote in the Nineteenth Century. They had brilliant insights but they lacked the statistical tools to test their ideas. Now that we have the tools and the historical data, there is no reason not to test and extend their ideas. One of the problems is figuring out what the Classics actually meant because their writing was verbose, obscure and difficult for modern readers to wade through.

Benjamin Higgins (1968) (here) has come to our rescue with a book (now out of print but still available used here) that develops a generalized mathematical model of economic development based on the classics (see Chapter 3). He presents eight structural equations (p. 63) and a time plot of the relationship between N (Population) and Q (GDP), above. His Figure 2-3 (above) looks very similar to the time series plot for the German 19th Century model (DEL19) at the beginning of this post which was based on an estimated dynamic state space model. The DEL19 model used the same variables identified by Higgins but did not arrive at the time plot using Higgins classical structural equations. Understanding how the DEL19 model was constructed will help me explain how to approach the Classics with modern tools.

Higgins identifies the following variables as central to the general Classical model: Production (Q), Labor (L), Capital (K), Wages (W), Profits (R), Investment (I)  and Technology (T). Variables can be further grouped (using Systems Theory) as system output state O=(L,Q,T), Endogenous (W,R,I), Exogenous (N) and Output (K) yielding the directed graph above (Higgins actual structural equations are presented below in the Notes--the endogenous variables can be reduced out of the equation system).

To Neoclassical Economists, the directed graph will look strange. Technology is usually taken as exogenous and the Capital stock would be included in the system state. But the Classics believed that Technology had to be embedded within investments and the Capital stock. Also, I think some Outputs are missing from Higgin's model (what happened to Adam Smith's Free Market? What happened to Democracy?) but I'll pick up the issue in a future post on the way to dealing with Liberalism and Neoliberalism.

The Classics also struggled with definitional issues. Did Capital include land, machines, buildings, knowledge, etc.? Were wages driven to subsistence in order to increase profits (R = Q - wL) where w is the subsistence wage. How to define Technology (T)? So many questions, so much speculation, so little testing.

Systems Theory avoids these arguments by defining the System State, S = S(Q,L,K,W,R,I,T), as being a function of all the essential variables in a system. The problem then is to estimate a state variable index and other independent indexes that describe Error Correcting Controllers (ECCs) for the system, that is, describe growth and control as two separate issues that have to be estimated separately for the system--allowing that the system might not be under adequate control.

The Measurement Matrix for the DEL19 state space model is presented above (for the moment, I am assuming that T is exogenous, but I'll pick up the issue in a future post). The first state variable, Classic1, describes overall growth (it's time plot is displayed at the beginning of this post). The second state variable, Classic2 = (0.86 N - 0.48 I), involves monitoring population growth relative to investment. The third state variable, Classic3 = (0.73 I - 0.47 L), involves monitoring investment relative to employment. The first three state variables explain over 99% of the variation in the indicators. The remaining three indicators deal mostly with wage controllers and explain little variance.

There are a number of interesting points about the estimated Measurement Matrix (estimated with Principal Components Analysis), The classics were very interested in Wages and Investment. But, they were also interested in the Capital Stock, K, and it played little role other than as an indicator of system growth in Germany (even though the Nineteenth and Twentieth Centuries are labeled as Capitalist--see below for more discussion in the Notes). 

In terms of system behavior, the steady state depicted in the DEL19 Time plot was not the result of the DEL19 BAU model but required input from the World System (see the directed graph above). Understanding that every economy is embedded within the World-System had to wait for the development of World-Systems Theory at the end of the Twentieth Century and the development of Hierarchical Control Systems in the 21st Century.

One other point about the time plot at the beginning of this post: WWI, the Great Depression and WWII are not explained by the forecast. In spite of the disruption of the Inter-War Years, we now know that the German Economy is starting to reach a steady state in the 21st Century (even though some Economists are labelling the approaching steady state as a crisis).

You can run both versions (unstable and stable) of the DEL19 Classic model here.

Summary

What can we learn from a Classical Model of German Development?

• It is not easy to just speculate and try to understand Complex Systems. The systems are Black Boxes that only reveal their behavior by observing inputs and outputs.
• Higgins Classical model (see below) is static whereas writers such as William Baumol (1960) thought the primary attribute of Classical Models were their "Magnificent Dynamics" (download pdf here).
• The Classics were willing to go ahead and speculate without clearly defining their essential variables, for example, Capital and Technology.
• The policy recommendations derived from Classical Models (Population control, Free Markets, Free Trade, Steady States, etc.) were advanced from weak foundations.
• The Classics did not advance ideas about how the Economic System is controlled, aside from free markets. In Germany, the Classical Economy was mostly controlled by Investment relative to population and employment. These two Error Correcting Controllers might be implicit in Classical reasoning but had to wait until a reinterpretation by Systems Theory in the Twentieth Century.
• The concept of the Steady State was dropped in favor of unlimited growth by Neoclassical Economics, but has been revitalized by Ecological Economics. Unfortunately, it is a state that might only be observe in the Future, and the Future is unknowable.
• Linkage to the World System is an important part of German development in the Late Nineteenth Century. Had the link been pursued, rather than World Domination, Germany would have become a stable society in the 20th and 21at Centuries. It would not have pursued the World Wars and the Great Depression would probably not have happened. However, there was no role for the World System in either Classical Economics or Neoclassical economics. World-Systems Theory was based in Classical Marxian Economics but borrowed freely from Neoclassical Economics when needed. There is more work to do in expanding the economic underpinnings of World-Systems Theory and Classical Economics is a good place to start.

Notes

Higgins (1968: 57) defines his Classical Economic System using structural-functional notation. The final equation, W = wL, is the long run constraint that wages are driven to subsistence, w. Structural equations are very important to Academic Economists, but there is a problem. The Cybernetic Theory of Isomorphic Systems proves that structural equations are not unique if two systems have the same time path for the output variables. In other words, The graphics at the beginning of this post look alike but they were generated from two different systems. The first graphic is from a state space model (DEL19W model) and the second from Higgins Classical model.

When we are studying complex systems such as macroeconomies,  we cannot hope to just speculate and specify structural equations. Economic systems are just two complex and the structural equations are unlikely to be unique, especially across countries. The Systems Theory argument is that the System State, which is unique to a given set of historical essential variables, must be estimated from system output data not theoretical speculations.

The role of the Capital Stock in understanding Capitalism is a case in point. One would think that the Capital stock would be critical to Capitalism and the ultimate Crisis of Capitalism. A little causal analysis will show it is just another output variable. First, the basic capital stock equation is K(t) = I - dK(t-1), that is, capital accumulates with Investment and becomes obsolete with depreciation, d. Since Investment comes out of Production, we have the causal diagram: 

If, for example, 20% of output is devoted to investment, i=0.20, and if depreciation is 20 years, d=1/20=0.05. If we solve this model:

we get K = 0.21 Q. To get unending, unstable Capital accumulation with this simple model would require that i / (1-k) > 1.0 and it simply can't be given that i and k are proportions < 1.0 in value. So, if we want to get unending capital accumulation, we need to look elsewhere. In a slightly expanded model:

All the graphs above can produce the same behavior for Q. The Capital stock (K) can be reduced out of the system. The important coefficient for the behavior of the system is q3 on the Q self-loop. If it is greater than 1.0, the system is unstable (exponential growth forever). If the system is stable, an equilibrium steady state will eventually be reached in the long-run when we are all dead. In other words, the steady state envisioned by Classical Economists can only result from stable economic systems, not systems that grow forever. And, instability must be driven either by unstable Malthusian population growth, by endogenous technological change (the self-loop on Q) or by exogenous Technological change, T.

What this all says to me is that (1) the contribution of a steady state, unique to Classical Economics, requires stable technological change and stable population growth, (2) The major omission of Classical (and Neoclassical) Economics is a role for the World System (I'll address the inclusion of the World System in a future post) and, (3) The historical data in a given country have to be allowed to speak for themselves so we can uncover the actual controllers of the Economic System, which need not be the same in every country.

Classic References

These works are available on line:

• Adam Smith Wealth of Nations
• Malthus An Essay on the Principal of Population
• Malthus Principles of Political Economy
• Ricardo Collected Works
• Marx Collected Works
• JS Mill Collected Works
• JM Keynes The Collected Writings

 

World-Systems Theory: The Malthusian Controller

 

When a Systems Theorists such as Kenneth Boulding (here) looks at the Malthusian Model he sees a General System, an interaction between population growth and economic development. When an Economist such as Harvey Leibenstein (here) looks at the model, he sees an Error Correcting Controller (ECC) for population and economic growth--sometimes Economists call the ECC a Stock Adjustment Model and use it for inventory modeling. When John Maynard Keynes looked at the Malthusian model, he saw a way to rebuild Economics on a more empirical basis rather than on Ricardian Theoretical Ideas (see Stefan Eich's analysis here and also note that Karl Marx's economic model  and Neoclassical Economic Theory were both based on Ricardo).

Why then is the Malthusian model so widely reviled even hated (Marx was harshly and implacably critical of Malthus and his ideas)? There are many reasons but basically Malthus was ahead of his time in the Social Sciences, articulating a model that was simple, easily testable and easily falsifiable. The assertion that population grows exponentially and agricultural production (subsistence) grows linearly (creating an eventual crisis), can be easily tested and rejected. In general, it didn't happened because of technological change in Agriculture.

Thomas Robert Malthus (1766-1834) had the misfortune of living during a period when the tools of the Classical Economists involved lengthy, obscure writings and poorly articulated mental models of the Economy. Abstract ideas were never given operational definition and as a result were untestable. Today, we have better tools to develop and test statistical models on historical data. When we read the Classics we need to salvage what is useful for model building and statistical testing. 

Harvey Leibenstein (1922-1994) did just that and developed the following equation which summarized Malthusian ideas:

where S is the system state at time t, Q is production, N is population and the c are constants.

As a causal directed graph (above), Technology (TECH) and dynamics (self-loops) for both Q and N can be added.

In a future post I'll define TECH better and test the entire Malthusian model during a specific period in a specific country, but first let me just concentrate on the Malthusian ECC on the right of the graph, S. Your first question should be "does the Malthusian ECC describe any historical period in a given country?". It actually describes many periods in many countries, but let me start with one I know well, Germany in the Late 19th Century.

The first line in the Measurement Matrix, above, describes overall growth in the system, Malthus1 = (0.707 QA + 0.707 N),  and  explains 87% of the variation in the two indicators. The second line of the Measurement matrix captures the Malthusian controller, Malthus2 = (0.707 QA - 0.707 N), and captures another 13% of the variation in Q and N, explaining all the variation.

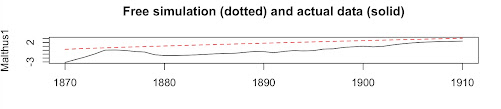
A time plot of Malthus2 (above) shows that right after German Unification in 1872, there was a Malthusian Crisis (QA-N < 0) that ran from Unification until almost 1880. The dashed red line in the graphic above is the attractor path for the Malthusian model, an approximate straight line around (QA-N = 0).

The result of this bounded Malthusian Crisis in Germany was that more than 5 million Germans emigrated to the US during the Late 19th Century, migration being one of the ways to alleviate Malthusian Pressure. European Emigration can be explained with other "pull factors" from the New World, but there also have to be "push factors," and Malthusian Pressure can be one. It is hard not to interpret the current Emigration from Africa to Europe as predominantly Malthusian Pressure, but it can be tested using the model above.

But what about Malthus1 that explains 87% of the variation in Q and N? The graphic above indicates that the Malthusian growth component was underperforming below the attractor path for most of the late 19th Century in Germany. Germany's late and rapid growth and Modernization, thought to be a factor in World War I, was basically a return to the attractor path interrupted by German Unification.

A question I'll answer in a later post is whether German development in the Late 19th Century had anything to do with feedback from the post-Unification Malthusian crisis? In other words, was there any feedback between Malthus2 and Malthus1? Answering the state-feedback question involves a more complicated causal direct graph (above) but can be handled easily by a state space model.

The mistake made by critics is to view the Malthusian ECC (Malthus2) as an all-or-nothing explanation. Clearly, it isn't. The ECC model above only explains 13% of the variation and we have only included two indicators, QA and N. In future posts, I will explain how the Malthusian Controller can be generalized to other controllers (for example, the Marxian controller (Q-W) and embedded within larger models. For the time being, my point is that we should salvage the Malthusian ECC from Classical arguments and realize that (1) it is one of many ECCs that exist within Modern Societies, (2) it still remains important for most pre-Industrial, pre-market societies that don't fit the Neoclassical Growth Model (as pointed out by Unified Growth Theory) and (3) it does provide, as Keynes thought, a way to rebuild economic models on more empirical footing.

In the mean time, if you want to run the DEL19 Malthusian model yourself, it is available here.

Methodology

The coefficients in the Malthusian Measurement matrix (above) were not plucked out of thin air or guesstimated but rather statistically estimated using Principle Components Analysis. The attractor path (dashed red line) was simulated using the DEL19 Malthusian model estimated with the dse package in the R programming language. You can run the DEL19 Malthusian model on line here using the Snippets web service.